krampus išao sam “varati” i napraviti geometrijsku konstrukciju i ispalo je da rjesenja ima beskonacno mnogo
Postavka zadatka: imamo tocke M i N i pravac SJ: x = 1.
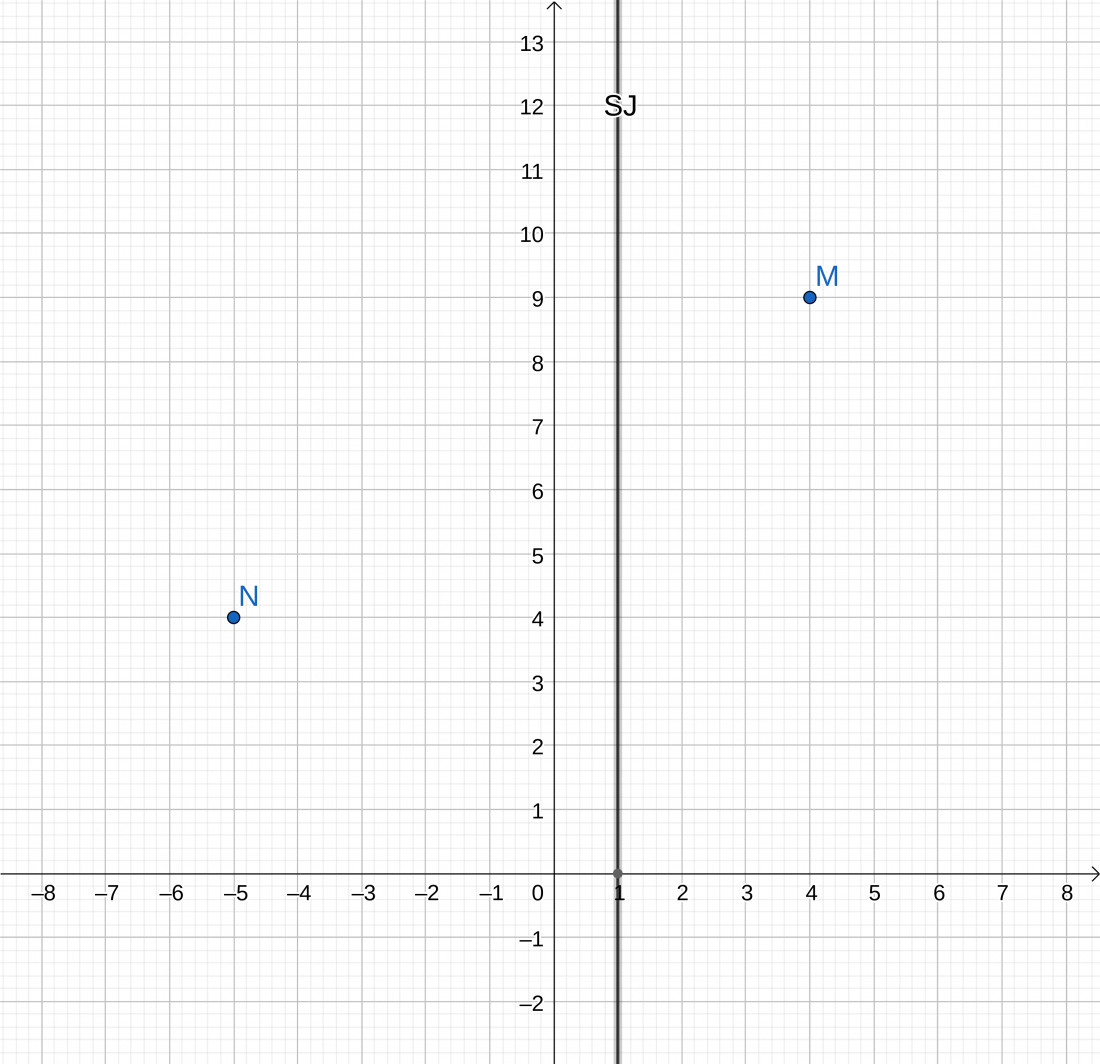
Treba naci tocku B tako da pravac BM i BN budu okomiti, jer su to upravo stranice kvadrata.
Easier done than said, zapravo, jer smo jos u osnovnoj ucili da ta tocka nuzno mora lezati na kruznici ciji je promjer razapet sa MN, also known as Talesov poucak.
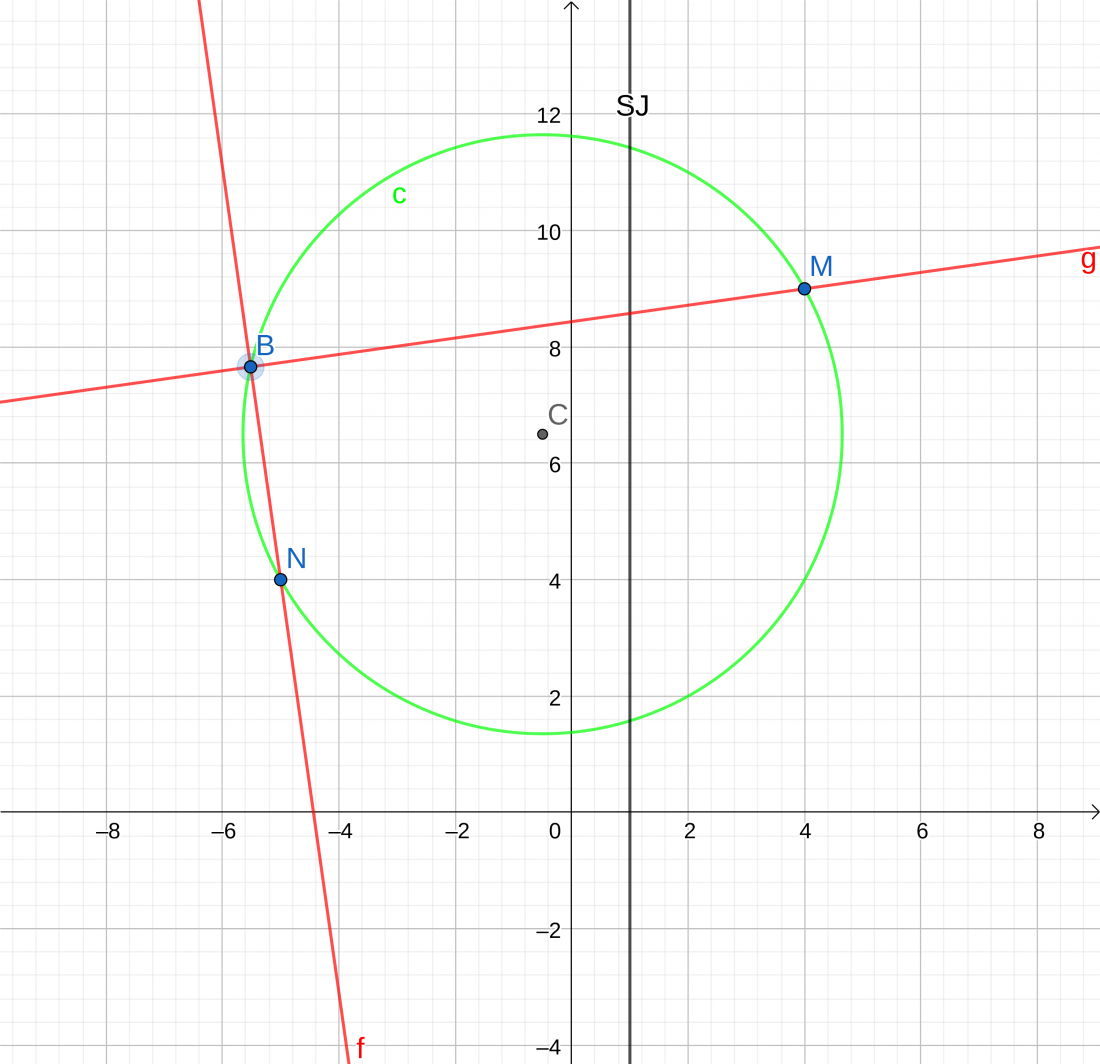
Uvodim tocku C koja je centar kruga i tocku B na kruznici. Vidi se da su BN i BM okomiti i to vrijedi za svaki B sa zelene kruznice.
No, ono sto je jos bitnije je da je tocka B zapravo vrh kvadrata jer stoji na presjeku dvije stranice kvadrata. A znas sto jos prolazi vrhom kvadrata? That’s right, dijagonala! Euklide, zvat ces me tatice!
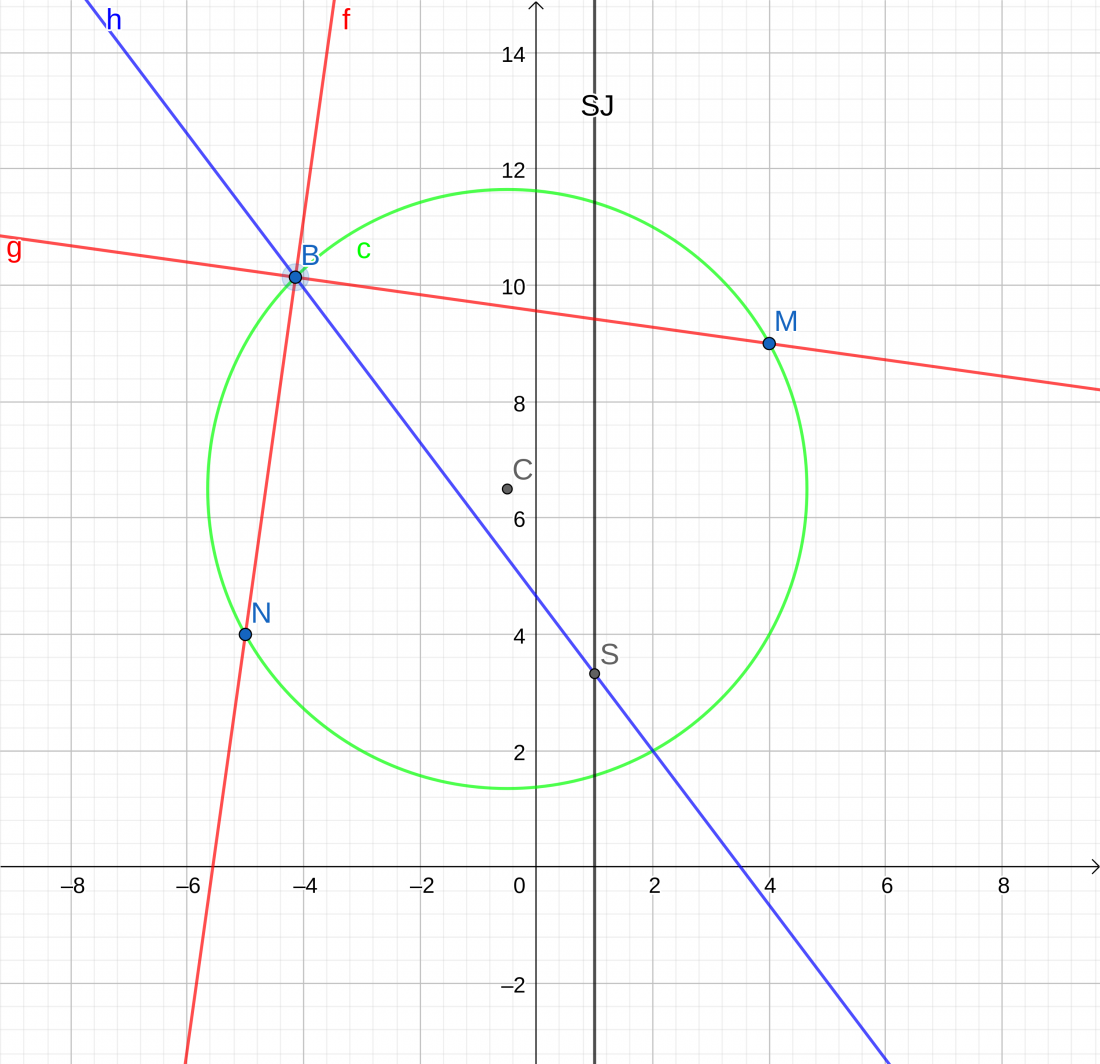
Napravio sam tzv Angle bisector koji prepolavlja kut izmedu dvije stranice, jer je to ono sto dijagonala kvadrata radi. Rezultirajuci pravac je plavi. Uz to, oznacio sam tocku S koja sjedi na pravcu x = 1. Ta tocka bi trebala biti sjeciste dijagonali - dakle sad iz te tocke mozemo nacrtati i drugu dijagonalu! Ona ce dakako biti pod pravim kutem hehe
Takoder sam malo pomako tocku B cist da se vidi da jos uvijek vrijedi tisucama godina star teorem. U svakom slucaju, druga dijagonala izgleda ovako:
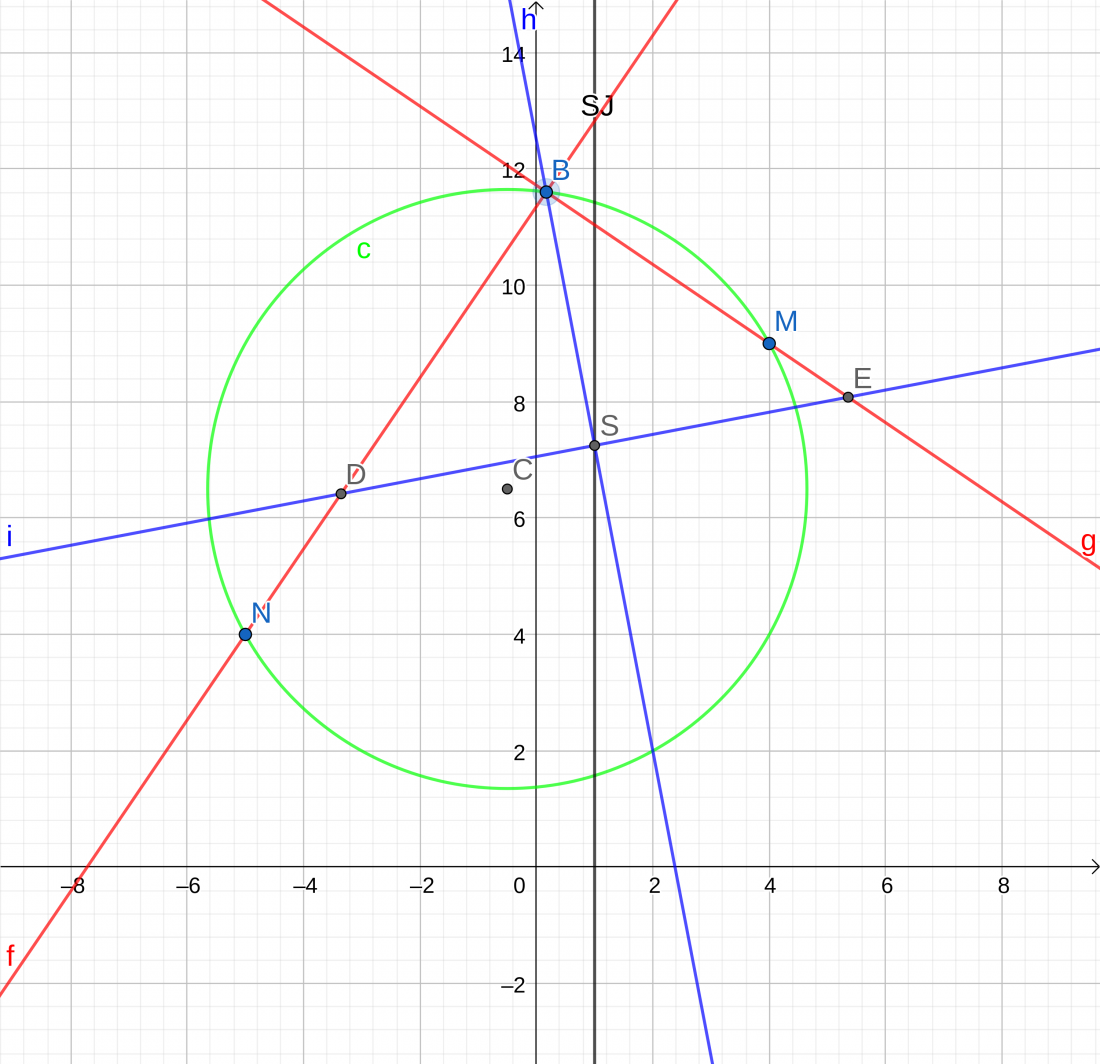
Sad je to sve malo polako crowdy, no zasad nismo naletili ni na kakve probleme u konstrukciji. Jos sam i oznacio tocke D i E gdje druga dijagonala sjece stranice - druga dva vrha kvadrata. Kao posljednji korak, povuci cu paralelu sa BM kroz tocku D i paralelu sa BN kroz tocku E kako bih nasao zadnju tocku kvadrata.
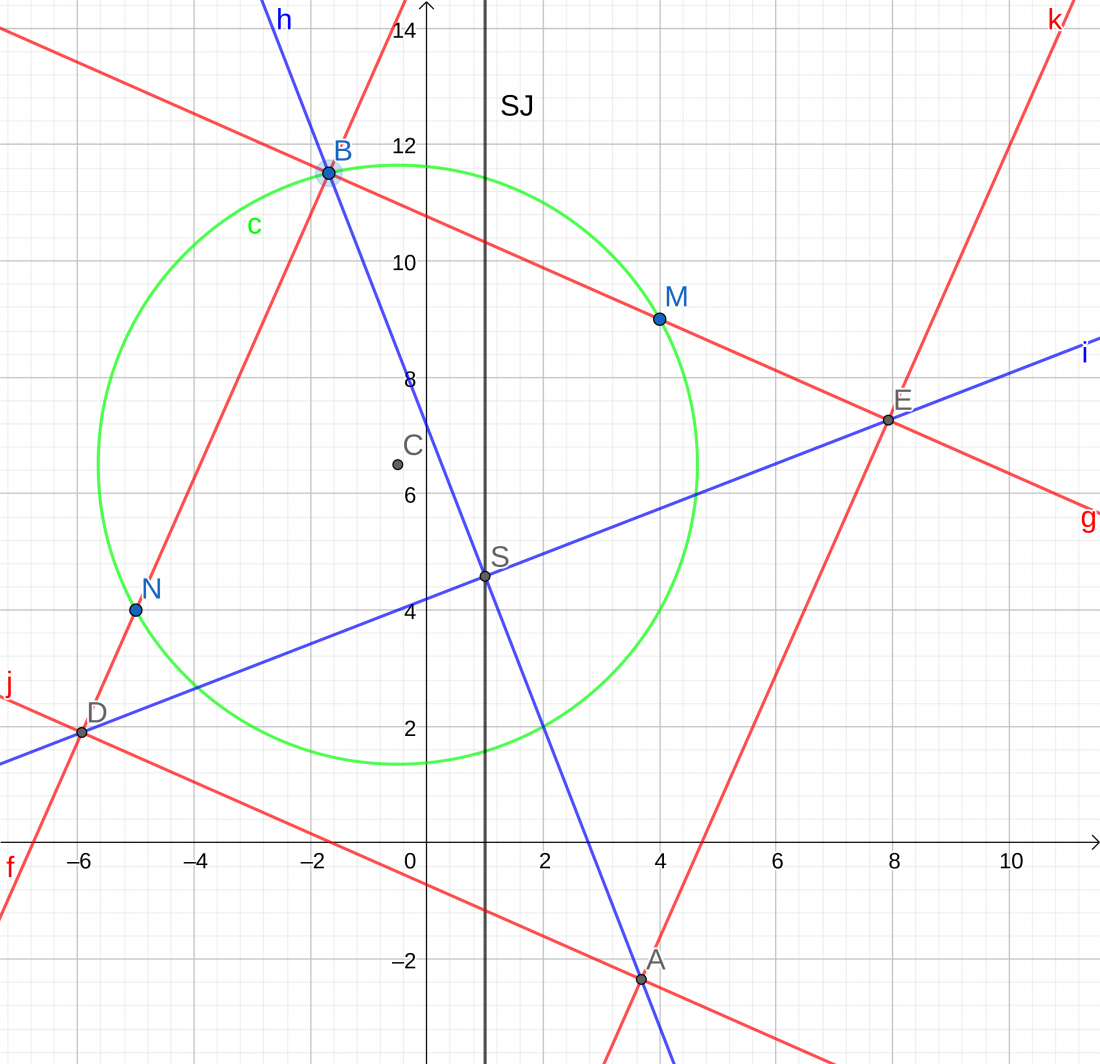
As it turns out, dobili smo kvadrat koji postuje sva ogranicenja koja su zadana u zadatku ali to rjesenje nije jedinstveno. Stovise postoji cijela dvoparametarska familija kvadrata koji zadovoljavaju constrainte (dvoparametarska zato jer ovisi iskljucivo o lokaciji tocke B na kruznici - mada kad bolje razmislim tehnicki je to jednoparametarska).
Nigdje se ne spominje da kvadrat mora biti skroz unutra, ili tangencijalan (to ni ne moze biti), ili jos nesto sto bi pomoglo svesti beskonacan skup rjesenja na samo dva.
Tako da, necu ni pokusavati sumnjati u svoje znanje geometrije (ofc) niti u implementacijske detalje geogebre, ali mozda bih se usudio cak reci da je zadatak krivo zadan. Euklid je ipak nakon svega moj tatica
Also ako itko pozeli se zajebavat s ovim sto sam crtao, .ggb fajl je ovdje