[STRUCE1] Gradivo

InCogNiTo124

Tko bumpa dokument SU2020/21 Zadaci iz zadaca i kvizova i zasto tocno?

vidraKida

AE
Eo lepi

vidraKida

Bananaking dobro bi nam to doslo. Ja sam raspisao formule i uvrstio sve, ali nisam bas nesto previse shvatio. Tako da mislim da mora bit neka glupa caka.

vidraKida

Ima netko postupak za ovaj zadatak?

gladiator

Ζ ε ύ ς

ovaj video https://ferhr.sharepoint.com/sites/SU120212022/Zajednicki%20dokumenti/Forms/AllItems.aspx?id=%2Fsites%2FSU120212022%2FZajednicki%20dokumenti%2FGeneral%2FRecordings%2FGeneral%2D20211220%5F102034%2DMeeting%20Recording%2Emp4&parent=%2Fsites%2FSU120212022%2FZajednicki%20dokumenti%2FGeneral%2FRecordings
na 4:20 ga asistent jako dobro objasni 🙂

ako ne mozes otvorit link onda nadi na teamsu snimku od predavanja 20.12 (ponedjeljak) pa pogledaj

Bananaking

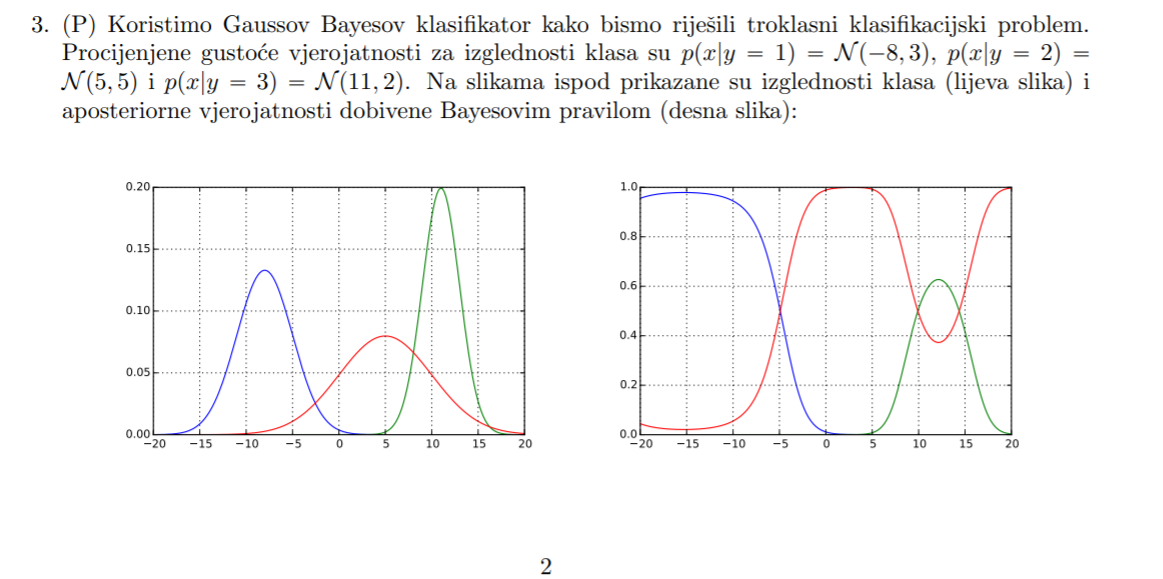
U ovom zadatku kaže nam da je na lijevoj slici izglednost klase, na desnoj aposteriorne vrijednosti

Bayesovo pravilo -> P(y|x) = P(x|y) * P(y) (uz izostavljeno P(x) jer je konstanta)

Nas zanimaju apriorne vjerojatnosti klasa odnosno P(y). Iz Bayesovog pravila P(y) = P(y|x) / P(x|y) odnosno aposteriorna vjerojatnost kroz izglednost, za sliku to je onda P(y) = desna slika / lijeva.

Iz danih varijanci i slike izglednosti zaključim da je plava linija “srednja” odnosno odgovara klasi y = 1 jer je za nju varijanca 3, između 5 (široke, crvene) i 2 ( zelene, uske)

Dakle idem gledati za plavu liniju desna slika / lijeva. Odaberem recimo x = -10, na lijevoj slici imam otprilike 0.105, na desnoj slici imam otprilike 0.95. Desna / lijeva je onda 0.95/0.105 = 9.04, a ne 0.1 koliko bi trebalo biti (lijeva / desna daje 0.1). Očito P(y = 1) ne može biti 9.04 ali gdje griješim u logici rješavanja?

InCogNiTo124

Bananaking zasto dijelis desnu sliku kroz lijevu?

Ugl desna slika je nastala kao \frac{f_i(x)}{f_1(x)+f_2(x)+f_3(x)}, gdje je i=1 plava klasa, i=2 crvena, a i=3 zelena. funkcije su svaki od grafića. dakle, nazivnik bayesa je suma tih funkcija. Nacrtas si u https://desmos.com/calculator ako zelis vizualizaciju kaj se dogada

Evo primjer: lijeva strana x=15, crveni gaus ima f(x) od 0.03 dok zeleni za isti x ima f(x) oko 0.02. plavi x je dovoljno malen da cu ga smatrat 0

Sta to znaci za desnu sliku: za x=15 gledaju se omjeri. Crvena boja je 0.03/(0.02+0.03) sto je oko 0.6, zelena ima 0.02/0.05 sto je oko 0.4, plavo je 0

InCogNiTo124

Bananaking cekaj ova slika nema smisla. Postoji pogreska u grafovima, nije velika ali je dovoljna da je krivo

Cubi

Bananaking Mucio sam se s ovim neko vrijeme i mislim da sam skuzio, pa da pokusam objasniti.
Znaci prva stvar, izostavio si p(x) na pocetku, a kasnije si trazio tocnu vrijednost od p(y|x) sto ne ide. P(x) se izostavlja pri maksimizaciji i usporedbi koja je vrijednost veća jer onda ta konstanta nema utjecaja.
E sad kako naci p(y). Kad bi sve vjerojatnosi p(y) bile jednake, onda bi desna slika izgledala drugacije. Plavi i crveni graf bi se sjekli na istom mjestu na lijevom i na desnom grafu. Npr. s lijeve slike se vidi da je vjerojatnost za primjer x=-4 veci za plavi graf. Međutim, da bi crvena klasa bila vjerojatnija tu, to mora znaciti da se plavi primjeri generiraju rijeđe, tj. da je p(y=plava) < p(y=crvena). Slicno i za ostale.
Kako naci tocne vrijednosti. Ja sam gledao sjecista na desnom grafu. Vidimo da se plavi i crveni graf sijeku u x=-5, tj. tu su jednako vjerojatni. Na lijevoj slici je vrijednost za x=-5 za plavi oko 0.7, a za crveni 0.1. Da bi bili jednako vjerojatni u x=-5 to znaci da crvena klasa mora biti 7 puta vjerojatnija od plave. I vec tu se otkriva odgovor, jedino moguce je 0.7 za crvenu i 0.1 za plavu. Isto razmisljanje moze se ponoviti za crveni i zeleni graf. Kod x=10 vidimo da je vrijednost za zeleni graf oko 0.17, a za crveni oko 0.5, znaci malo vise od 3 puta manja. Znaci vjerojatnost za crvene primjere mora biti malo vise od 3 puta vjerojatnija od zelenog. 0.7 i 0.2 odgovaraju tome.

Malo je objasnjenje zbrda zdola, al nadam se da ce pomoci. Mogu pokusati objasniti neki detalj ako bude potrebno.

Tootha

Bananaking Možeš rješiti i računanjem apriornih vjerojatnosti iz sjecišta desnog grafa.
U x = -5 vrijedi P(y=1)P(x=-5 | y=1) = P(y=2)P(x=-5 | y = 2). Nazivnik se ovdje može maknuti jer je jednak za oba slučaja.
U x = 10 vrijedi P(y=2)P(x=10 | y=2) = P(y=3)P(x=10 | y=3). Izglednosti u ovim jednadžbama možeš dobiti egzaktno preko formule za Gaussovu distribuciju. Kada dobiješ te vrijednosti možeš izraziti P(y=1) i P(y=3) preko P(y=2). Iskoristi još P(y=1) + P(y=2) + P(y=3) = 1 da dobiješ P(y=2) i preko toga dobiješ P(y=1) i P(y=3).

Napomena:
U zadatku koriste notaciju N(mi, sigma)] umjesto N(mi, sigma²).

Mikki

InCogNiTo124 Nije li da bi ovo tvoje vrijedilo da je lijevi graf zajednička gustoća p(x,y), a ne p(x|y)?

bodilyfluids

InCogNiTo124 di

InCogNiTo124

Dragi prijatelj strojnog učenja na x=15 lijevo je zeleno vece, a na x=15 desno je crveno vece i to nije dobro

evo tu sam nacrtao

https://www.desmos.com/calculator/cd8ietcxvg

InCogNiTo124

Mikki vidi graf iznad

gad_gadski

studoš snajder pojasnio zadatak na predavanju u srijedu ovu zadnju, imas na temsu

Heklijo

Jel se kod odredivanja topoloskog uredaja gleda po razinama? Npr. prvo nodes koji nemaju parent (w,y) pa zatim njihova djeca (z, x) itd…

Jel bi onda TU bio : W, Y, X, Z?

Bananaking

Geralt of Rivia Tako je

Tompa007

zasto je tu D tocno ? a ne C?

bodilyfluids

𝐓𝐇𝐄 𝐒𝐄𝐂𝐑𝐄𝐓 - 𝐂𝐋𝐔𝐁 na predavanju je rješen, ugl imaš rubni slučaj kada je N=2, i tada slijedi mi1 = mi3, dakle ne vrijedi stroga nejednakost

Bananaking

𝐓𝐇𝐄 𝐒𝐄𝐂𝐑𝐄𝐓 - 𝐂𝐋𝐔𝐁 map procjena je ( Nk + Alfak - 1 ) / (Suma-po-k(Nk + Alfak) - K)

N1 = 0, N2 = ½ N, N3 = ½ N
Alfa1 = 2, Alfa2 = 2, Alfa3 = 1

Kad uvrstiš dobiješ

mi(MAP, 1) = 1 / N + 2
mi(MAP, 2) = 0.5 N + 1 / N + 2
mi(MAP, 3) = 0.5N / N + 2

N je broj primjera, Nk je broj nastupanja k-te vrijednosti. I sad u N staviš najmanji mogući N=1 i dobiješ za 1 -> ⅓, za 2 -> ½, za 3 -> ⅙

Pod c) kaže da je mi3 uvijek veći od mi1 (što vidiš gore da nije točno)
Pod d) kaže da je:

mi1 od 0 do ⅓ (za N = 1 je ⅓, za veći N se smanjuje)
mi2 između 0.5 i 1 (za N = 1 je 0.5, za veći raste ali ne može biti veći od jedan jer se N u brojniku dijeli sa 2 a u naz ne)
da je mi2 uvijek veći od mi3 i da su između 0 i 1 ( mi2 ima taj “+1” u brojniku)

Voila.

Tompa007

Dragi prijatelj strojnog učenja ahaaaa, mislis kada je N =1 ? pa onda moze biti da je mi1 = mi2 ili mi1 = mi3 ovisno koja realizacija se dogodila

« Prethodna stranica Sljedeća stranica »