Ovako sam rješavala simplex metodu za jednu knjigu pa ako će kome pomoć i bit malo jasnije 🙂
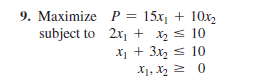
To turn the i-system into an e-system, add slack variables to the left side of the problem constraint inequalities.
The slack variable $s$ is the difference between the left and right sides of inequality so if we add it to the left side, the inequality sign becomes a sign of equality.
There are two problem constraint inequalities, so we will add $s_1$ to the first one and $s_2$ to the second one.
\begin{aligned}
2x_1+x_2 +s_1&=10&&\text{}\\
x_1+3x_2 +s_2&=10&&\text{}\\
\end{aligned}
To complete the initial system, move terms on the left of the objective function equation to the right.
-15x_1-10x_2+P=0
(B)
Fill the matrix with coefficients from Step 2 to get the initial simplex tableau.
Label rows in tableau with basic variables, $s_1,s_2, P$ in such a way that the intersection element of the same label row and column is 1.
\begin{array}{rcl}
&\\
&\begin{array}{c}&x_1&x_2&s_1&s_2&P&&\end{array}\hspace{1em} \\ \begin{matrix}s_1\\ s_2\\ P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}2& \phantom{-}1&1 & 0 &0 &\big| & 10&\\
&\phantom{-}1& \phantom{-}3&0& 1 & 0 &\big| & 10 &\\\hdashline
&-15& -10&0 &0& 1 &\big| &0& \\\end{bmatrix}
&\hspace{-0.5em}
\\ &\end{array}
The column with the most negative indicator is called the pivot column. The label of that column is called entering variable.
Divide each element in the last column with corresponding positive ones in the pivot column. The row in which the smallest quotient is obtained is called the pivot row. The label of that row is called the exiting variable.
\begin{array}{rcl}
&\begin{array}{c} \scriptstyle Entering\;variable&&&&&&&&\end{array}\\
&\begin{array}{c}\downarrow&&&&&&&&&&\end{array}\\
&\begin{array}{c}&x_1&x_2&s_1&s_2&P&&\end{array}\hspace{1em} \\ \begin{matrix}\scriptstyle Exiting\;variable\displaystyle \rightarrow&s_1\\ &s_2\\ &P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}2& \phantom{-}1&1 & 0 &0 &\big| & 10&\\
&\phantom{-}1& \phantom{-}3&0& 1 & 0 &\big| & 10 &\\\hdashline
&-15& -10&0 &0& 1 &\big| &0& \\\end{bmatrix}
&\hspace{-0.5em}
\begin{matrix} \frac{10}{2}=5\phantom{..} \\\\\frac{10}{1}=10\\\ \end{matrix}\hspace{-0.5em}
\\ &\end{array}
The first column is the pivot column. The first row is the pivot row.
The pivot element is placed at the intersection of the pivot column and pivot row and it is circled in the tableau below.
\begin{array}{rcl}
&\begin{array}{c} \scriptstyle Entering\;variable&&&&&&&&\end{array}\\
&\begin{array}{c}\downarrow&&&&&&&&&&\end{array}\\
&\begin{array}{c}&x_1&x_2&s_1&s_2&P&&\end{array}\hspace{1em} \\ \begin{matrix}\scriptstyle Exiting\;variable\displaystyle \rightarrow&s_1\\ &s_2\\ &P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}\textcircled{2}& \phantom{-}1&1 & 0 &0 &\big| & 10&\\
&\phantom{-}1& \phantom{-}3&0& 1 & 0 &\big| & 10 &\\\hdashline
&-15& -10&0 &0& 1 &\big| &0& \\\end{bmatrix}
&\hspace{-0.5em}
\\ &\end{array}
Index of the pivot element is $(1,1)$.
Entering variable is $x_1$.
Exiting variable is $s_1$.
©
Perform pivot operation. $R$ represents a row.
\begin{array}{rcl}
&\\
&\begin{array}{c}&x_1&x_2&s_1&s_2&P&&\end{array}\hspace{1em} \\ \begin{matrix}s_1\\ s_2\\ P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}\textcircled{2}& \phantom{-}1&1 & 0 &0 &\big| & 10&\\
&\phantom{-}1& \phantom{-}3&0& 1 & 0 &\big| & 10 &\\\hdashline
&-15& -10&0 &0& 1 &\big| &0& \\\end{bmatrix}
&\hspace{-0.5em}
\begin{matrix} \frac{R_1}{2}\scriptstyle\to R_1\phantom{...} \\ \\ \\\end{matrix}\hspace{-0.5em}
\\ &\end{array}
\begin{array}{rcl}
&\\
&\begin{array}{c}&x_1&x_2&s_1&s_2&P&&\end{array}\hspace{1em} \\ \begin{matrix}&s_1\\ \sim& s_2\\ &P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}\textcircled{1}& 0.5&0.5 & 0 &0 &\big| & 10&\\
&\phantom{-}1& \phantom{-}3&0& 1 & 0 &\big| & 10 &\\\hdashline
&-15& -10&0 &0& 1 &\big| &0& \\\end{bmatrix}
&\hspace{-0.5em}
\begin{matrix} \\ \scriptstyle -R_1+R_2\to R_2 \\ \scriptstyle 15R_1+R_3\to R_3 \end{matrix}\hspace{-0.5em}
\\ &\end{array}
\begin{array}{rcl}
&\\
&\begin{array}{c}&&x_1&&x_2&&s_1&s_2&P&&&&\end{array}\hspace{1em} \\ \begin{matrix}&s_1\\ \sim& s_2\\ &P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}\textcircled{1}& \phantom{-}0.5&\phantom{-}0.5& 0 &0 &\big| & 10&\\
&\phantom{-}0& \phantom{-}2.5&-0.5& 1 & 0 &\big| & 0 &\\\hdashline
&\phantom{-}0& -2.5&\phantom{-}7.5 &0& 1 &\big| &150& \\\end{bmatrix}
&\hspace{-0.5em}
\begin{matrix} \\ \phantom{\scriptstyle -1R_1+R_2\to R_2} \\ \end{matrix}\hspace{-0.5em}
\\ &\end{array}
—————–
Since there are negative indicators in the bottom row, repeat the whole procedure explained in (B).
New basic variables are $x_1,s_2,P.$ Relabel the rows.
\begin{array}{rcl}
&\begin{array}{c} \scriptstyle Entering\;variable&&&&&&&&\end{array}\\
&\begin{array}{c}\downarrow&&&&&&&\end{array}\\
&\begin{array}{c}&&x_1&&x_2&&s_1&s_2&P&&&&\end{array}\hspace{1em} \\ \begin{matrix}&x_1\\\scriptstyle Exiting\;variable\displaystyle \rightarrow& s_2\\ &P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}1& \phantom{-}0.5&\phantom{-}0.5& 0 &0 &\big| & 10&\\
&\phantom{-}0& \phantom{-}\boxed{2.5}&-0.5& 1 & 0 &\big| & 0 &\\\hdashline
&\phantom{-}0& -2.5&\phantom{-}7.5 &0& 1 &\big| &150& \\\end{bmatrix}
&\hspace{-0.5em}
\begin{matrix} \frac{10}{0.5}=20\phantom{..} \\\\\frac{0}{2.5}=0\phantom{....} \\\\ \end{matrix}\hspace{-0.5em}
\\ &\end{array}
Index of the pivot element is $(2,2)$.
Entering variable is $x_2$.
Exiting variable is $s_2$.
Perform pivot operation.
\begin{array}{rcl}
&\\
&\begin{array}{c}&&x_1&&x_2&&s_1&s_2&P&&&&\end{array}\hspace{1em} \\ \begin{matrix}\phantom{...}&x_1\\& s_2\\ &P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}1& \phantom{-}0.5&\phantom{-}0.5& 0 &0 &\big| & 10&\\
&\phantom{-}0& \phantom{-}\boxed{2.5}&-0.5& 1 & 0 &\big| & 0 &\\\hdashline
&\phantom{-}0& -2.5&\phantom{-}7.5 &0& 1 &\big| &150& \\\end{bmatrix}
&\hspace{-0.5em}
\begin{matrix} \\ \frac{R_2}{2.5}\scriptstyle\to R_2\phantom{...} \\ \\\end{matrix}\hspace{-0.5em}
\\ &\end{array}
\begin{array}{rcl}
&\\
&\begin{array}{c}&&x_1&&x_2&&s_1&s_2&P&&&&\end{array}\hspace{1em} \\ \begin{matrix}&x_1\\\sim & s_2\\ &P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}1& \phantom{-}0.5&\phantom{-}0.5& 0 &0 &\big| & 10&\\
&\phantom{-}0& \phantom{-}\boxed{1}&-0.2&0.4 & 0 &\big| & 0 &\\\hdashline
&\phantom{-}0& -2.5&\phantom{-}7.5 &0& 1 &\big| &150& \\\end{bmatrix}
&\hspace{-0.5em}
\begin{matrix} \scriptstyle -0.5R_2+R_1\to R_1 \\ \\ \scriptstyle 2.5R_2+R_3\to R_3 \end{matrix}\hspace{-0.5em}
\\ &\end{array}
\begin{array}{rcl}
&\\
&\begin{array}{c}&\;x_1&&x_2&&s_1&&s_2&&P&&&&\end{array}\hspace{1em} \\ \begin{matrix}&x_1\\\sim & s_2\\ &P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}1& \phantom{-}0&\phantom{-}0.1& -0.2 &0 &\big| &\phantom{-}10&\\
&\phantom{-}0& \phantom{-}\boxed{1}&-0.2&\phantom{-} 0.4 & 0 &\big| & \phantom{-}0 &\\\hdashline
&\phantom{-}0& \phantom{-}0&\phantom{-}7&\phantom{-}1& 1 &\big| &\phantom{-}75& \\\end{bmatrix}
&\hspace{-0.5em}
\begin{matrix} \\ \phantom{\scriptstyle -2.5R_1+R_2\to R_2} .\\ \end{matrix}\hspace{-0.5em}
\\ &\end{array}
——————–
New basic variables are $x_1,x_2,P.$ Relabel the rows.
\begin{array}{rcl}
&\\
&\begin{array}{c}&\;x_1&&x_2&&s_1&&s_2&&P&&&&\end{array}\hspace{1em} \\ \begin{matrix}&x_1\\& x_2\\ &P\end{matrix}\hspace{-0.5em}
&\begin{bmatrix}
&\phantom{-}1& \phantom{-}0&\phantom{-}0.1& -0.2 &0 &\big| &\phantom{-}10&\\
&\phantom{-}0& \phantom{-}1&-0.2&\phantom{-} 0.4 & 0 &\big| & \phantom{-}0 &\\\hdashline
&\phantom{-}0& \phantom{-}0&\phantom{-}7&\phantom{-}1& 1 &\big| &\phantom{-}75& \\\end{bmatrix}
&\hspace{-0.5em}
\begin{matrix} \\ \phantom{\scriptstyle -2.5R_1+R_2\to R_2} .\\ \end{matrix}\hspace{-0.5em}
\\ &\end{array}
————————
There are no negative indicators in the last row, therefore we can read optimal solution from the tableau.
Read row labels with corresponding elements to the right of the vertical line to obtain a solution.
Max $P=75$ at $x_1=10$ and $x_2=0$